| M1 |
|
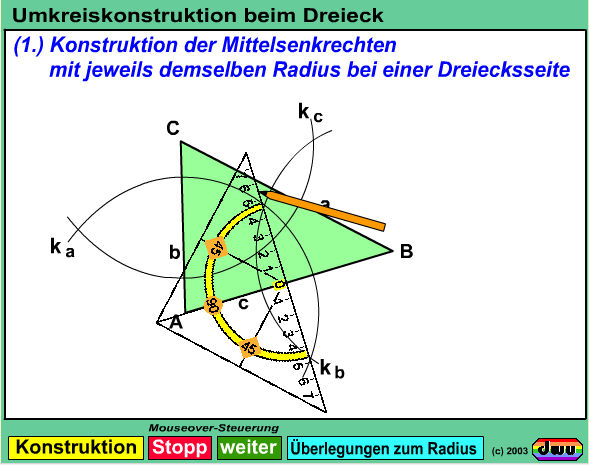
Die Konstruktion des Umkreises beim Dreieck
erfolgt über die Mittelsenkrechten ma,mb und mc, die sich in einem gemeinsamen Punkt M,
dem Umkreis-Mittelpunkt schneiden.
Der Radius r des Umkreises wird hier über die Strecken x, y und z weiter verdeutlicht.
Einer der Endpunkte dieser Strecken ist dabei zugleich Eckpunkt des Dreiecks, der andere bewegt sich auf der entsprechenden Mittelsenkrechten
in das Dreieck hinein. Dabei werden die Stecken x, y und z ständig länger, bis sie dabei im Punkt M gleichlang geworden sind.
Also haben die Eckpunkte A, B und C des Dreiecks zum Punkt M denselben Abstand und man kann den Umkreis des Dreiecks zeichnen.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M2 |
|
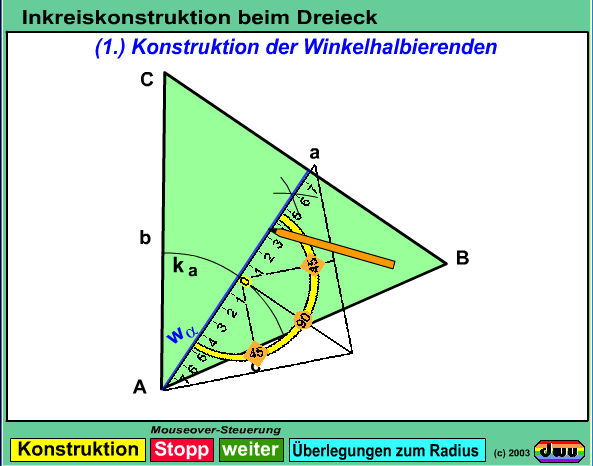
Die Konstruktion des Inkreises beim Dreieck erfolgt über die Winkelhalbierenden
wAlpha, wBeta und wGamma, die
sich in einem gemeinsamen Punkt O, dem Inkreis-Mittelpunkt schneiden.
Der Radius Rho des Inkreises wird hier über drei bewegliche Kreise weiter verdeutlicht, deren Mittelpunkte sich jeweils von einem der
Dreiecks-Eckpunkte aus auf der Winkelhalbierenden in das Dreieck hineinbewegen.
Diese drei Kreise berühren immer schon zwei Dreiecksseiten, werden immer größer, bis sie im Punkt O aufeinander liegen und somit
gleichgroß sind. Dann berührt dieser Kreis alle Dreiecksseiten und ist somit der Inkreis des Dreiecks.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M3 |
|
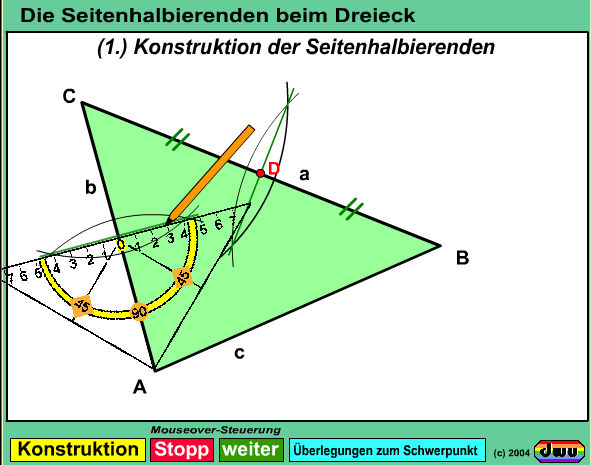
Die Seitenhalbierenden des Dreiecks sind die Verbindungslinien der Eckpunkte mit den Mittelpunkten der Gegenseiten.
Sie schneiden sich in einem gemeinsamen Punkt S, dem Schwerpunkt, dessen Eigenschaften sich mit dem Hebelgesetz der Physik erklären lassen.
Die Seitenhalbierenden des Dreiecks teilen sich jeweils im Verhältnis 2:1 (2/3 Abstand bis zum Eckpunkt und 1/3 Abstand bis zum jeweiligen Seiten-Mittelpunkt).
Wegen dieses Abstandsverhältnisses kann ein Dreieck im Schwerpunkt S ausbalanciert werden, weil dabei in alllen denkbaren Richtungen (z.B. auf sa, ...) der linke Teil "gleichschwer" wie der rechte Teil ist. Voraussetzung dafür ist die Anfertigung des Dreiecks aus einem "homogenen" Material gleichbleibender Schichtstärke.
Die Höhenlinien des Dreiecks sind die Senkrechten zu den Dreiecksseiten an die jeweils gegenüberliegenden Eckpunkte. Sie schneiden sich in einem gemeinsamen Punkt H, dem Höhenschnittpunkt.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M4 |
|
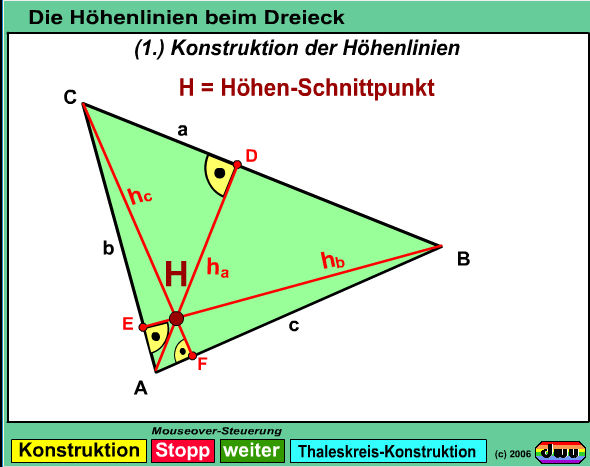
Die Höhenlinien des Dreiecks sind die Senkrechten zu den Dreiecksseiten an die jeweils gegenüberliegenden
Eckpunkte. Sie schneiden sich in einem gemeinsamen Punkt H, dem Höhenschnittpunkt. Die Konstruktion kann mit dem Geodreieck erfolgen,
oder aber mit den "klassischen" Geometriegeräten Zirkel und Lineal z.B. durch mehrfache Anwendung des Satzes von Thales.
Genau genommen genügt dabei die Konstruktion von zwei Höhenlinien, um den Schnittpunkt H zu erhalten.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M5 |
|
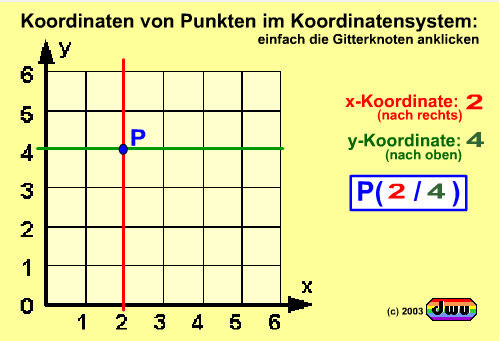
Die Punkte im Koordinatensystem werden in der Regel in der Koordinatenschreibweise (x/y) bezeichnet,
so dass man die Lage jedes Punktes über die x-Koordinate (Rechts-Wert) und die y-Koordinate (Hoch-Wert) kennt.
Die Gitterpunkte dieses Koordinatensystems sind anklickbar, so dass alle ganzzahligen Koordinaten von jeweils 0 bis 6 dargestellt werden können.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M6 |
|
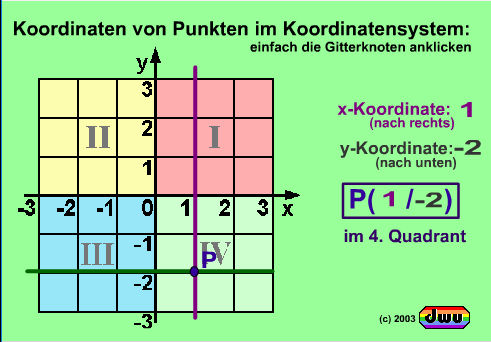
Das Koordinatensystem der Ebene ist in die 4 Quadranten I, II, III und IV aufgeteilt.
In der Koordinatenschreibweise werden alle Punkte P(x/y) je nach Quadrant mit positiven oder negativen Koordinaten bezeichnet. Dabei gilt . . . 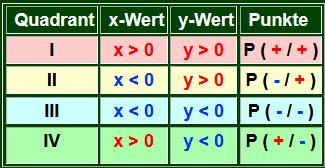
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M7 |
|
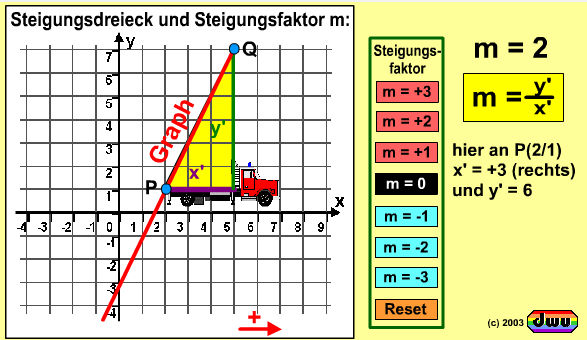
Den Steigungsfaktor der linearen Funktion kann man sich über das Feuerwehrauto-Modell verdeutlichen.
Je steiler die Leiter des Feuerwehrautos ausgerichtet wird, desto größer ist auch der Steigungsfaktor m.
Der Steigungsfaktor ist positiv, wenn das Fahrzeug in x-Richtung, also nach rechts fährt und negativ, wenn es nach links fährt.
Die Steigungsfaktoren +3, … -3 sind anklickbar.
Das Feuerwehrauto fährt dann zur Einsatzstelle P des zu erstellenden Graphen, konstruiert den Punkt Q und das Steigungsdreieck und damit dann den Graphen im Koordinatensystem.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M8 |
|
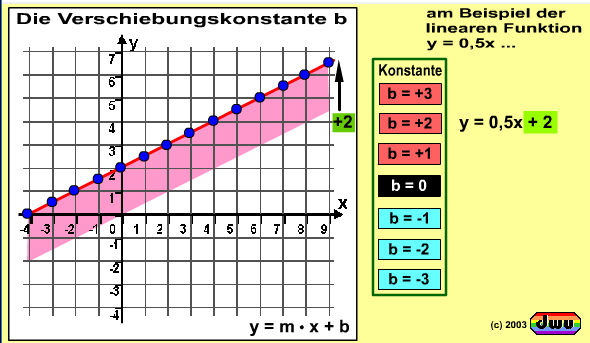
Die Verschiebungskonstante der linearen Funktion gibt an, um wieviel alle Punkte des Graphen nach oben
(b positiv) oder nach unten (b negativ) verschoben sind.
Die Werte der Verschiebungskonstanten +3, … -3 sind anklickbar. Die dargestellten Punkte verschieben sich dann entsprechend und somit der
gesamte Graph.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M9 |
|
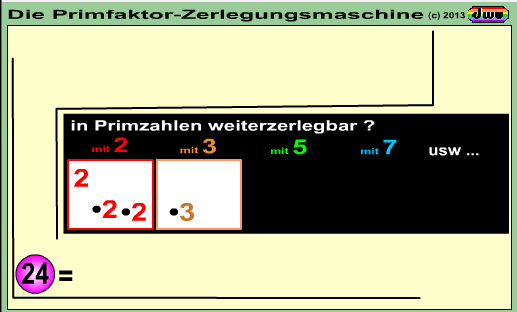
Bei der Primfaktor-Zerlegung wird eine Zahl zunächst so oft als möglich durch 2, dann durch 3,
dann durch 5 ... geteilt, bis sie vollständig in ein Produkt aus Primzahlen zerlegt ist.
Diese Animation zeigt den Ablauf der Primfaktorzerlegung an den Beispiel-Zahlen 8; 10; 12; 15; 24 und 36 auf.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M10 |
|
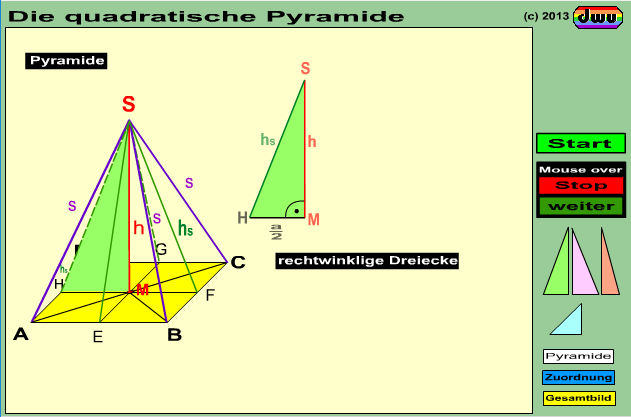
Die Berechnung der Linien einer quadratischen Pyramide kann über vier verschiedene rechtwinklige
Teildreiecke erfolgen. In dieser Animation wird zunächst in der Grundfläche ein Quadrat bezeichnet.
Anschließend wird daraus eine Pyramide gebildet. Es folgt dann die Visualisierung der 4 verschiedenen Teildreiecke zur Berechnung dieser Pyramide.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M11 |
|
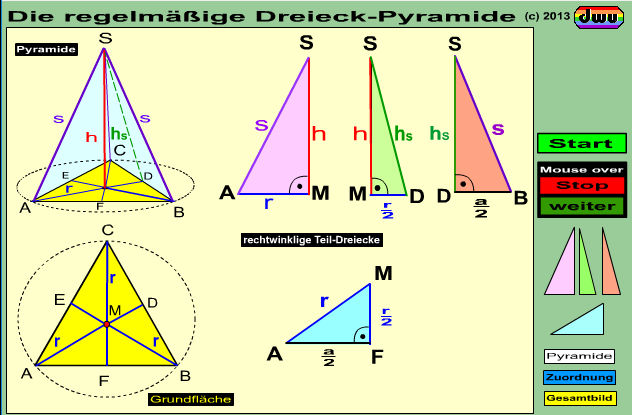
Die Berechnung der Linien einer regelmäßigen Dreieck-Pyramide kann über vier verschiedene
rechtwinklige Teildreiecke erfolgen. In dieser Animation wird zunächst mit dem Radius r in der Grundfläche ein gleichseitiges Dreieck konstruiert.
Anschließend wird daraus eine Pyramide gebildet. Es folgt dann die Visualisierung der 4 verschiedenen Teildreiecke zur Berechnung dieser Pyramide.
Da sich die Seitenhalbierenden des Dreiecks im Verhältnis 2:1 teilen, haben bei der rm. Dreieckpyramide die innen auf der Grundfläche verlaufenden
Katheten die Längen r (= Radius) und r/2 (= halber Radius).
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M12 |
|
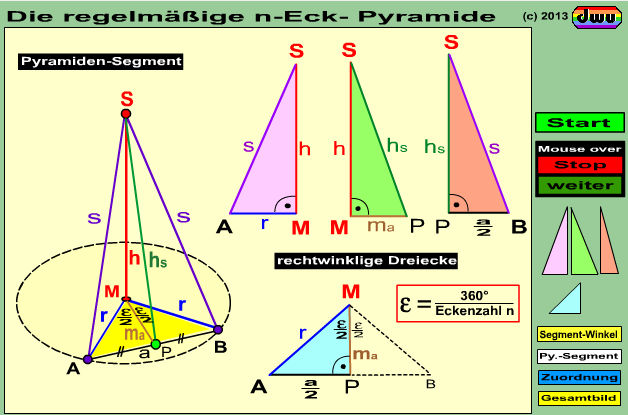
Die Berechnung der Linien einer allgemeinen regelmäßigen Pyramide kann über vier verschiedene
rechtwinklige Teildreiecke erfolgen. In dieser Animation wird zunächst mit dem Radius r in der Grundfläche das Segmant-Dreieck ABM mit dem
Öffnungswinkel ε konstruiert. Anschließend wird daraus ein allgemeines Pyramiden-Segment gebildet.
Es folgt dann die Visualisierung der 4 verschiedenen Teildreiecke zur Berechnung dieser Pyramide.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
| M13 |
|
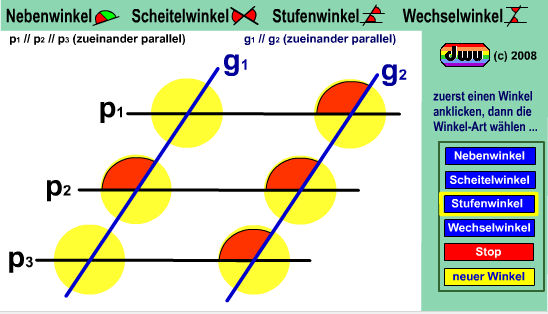
Nebenwinkel sind Winkel, die nebeneinander liegen und zusammen einen gestreckten Winkel (180°) ergeben. Beim Schnitt zweier Geraden nennt man jeweils zwei sich gegenüber stehende Winkel Scheitelwinkel. Sie sind immer gleichgroß.
Schneidet eine Gerade mehrere Parallelen, so entstehen gleichgroße Stufenwinkel und Wechselwinkel.
Die interaktive Animation ist im Mathematik-Paket enthalten ...
| |
 |