Infos zum Satz des Pythagoras:

---

Ausgangsfigur und Begriffe:		Der Satz des Pythagoras kann nur in einem  rechtwinkligen Dreieck   angewandt werden.
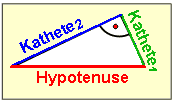
		Die Seiten eines rechtwinkligen Dreiecks werden mit folgenden "alten" griechischen Namen bezeichnet: Die beiden Schenkel des rechten Winkels heissen Katheten Hier als  Kathete1  und  Kathete2  bezeichnet. Die Gegenseite zum rechten Winkel nennt man  Hypotenuse . Die Hypotenuse ist die längste Seite im rechtwinkligen Dreieck.

---

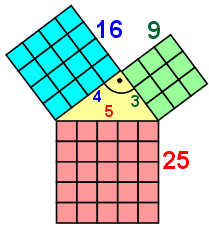Satz des Pythagoras :		Ein Dreieck mit dem Seitenverhältnis 3 : 4 : 5 ist immer ein rechtwinkliges Dreieck. Man bezeichnet daher die drei zusammengehörenden Zahlen (3;4;5) als pythagoräisches Zahlentrippel (3-Zahlen). Der Grund dafür ist in der Skizze erkennbar.   25    =    9    +    16   oder   5²    =    3²    +    4²   Allgemein gilt ...   Hypotenuse²    =    Kathete1²    +    Kathete2²   In der Wurzel-Form gilt damit ...   Hypotenuse   =    Kathete1² + Kathete2²
Die oftmals "übliche" Formel a² + b² = c² wird hier nicht verwendet, weil die Seiten rechtwinkliger   Teildreiecke eigentlich meist anders bezeichet sind.
Die interaktiven Übungen beziehen sich auf die Wurzelform.  Ist die  Hypotenuse gesucht , so steht in der Wurzel die  Summe der Kathetenquadrate ,  ist eine  Kathete gesucht , so muss  vom Hypotenusen-Quadrat subtrahiert  werden.

---

Allgemeine Tipps: Mit der Tabulatortaste gelangt man jeweils ins jeweils nächste Eingabefeld der Übungsaufgaben. Leerzeichen werden als Fehler gewertet und 100% gibt es nur, wenn vor dem Prüfen alle Felder richtig ausgefüllt sind. Die Eingabe von Hochzahlen kann über die Sonderzeichen ² bzw ³ über [Alt Gr] + [2] bzw. [3] erfolgen, oder für alle denkbaren Hochzahlen mit der Hochzahltaste

Diese Seite drucken

© 2006

Fenster schließen