Infos zur quadratischen Funktion:

Fenster schließen

---

Reinquadratische Funktion:   Wenn die Lösungsvariable (x) nur in der 2. Potenz vorkommt
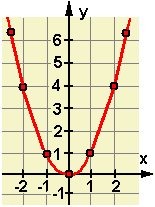	Der Graph einer reinquadratischen Funktion ist eine Parabel, die nur in der y-Richtung verschoben sein kann.  Parabel-Art  Funkt.-Gleichung Verschiebungskonstante  Normalparabel  (wie abgebildet)  y = x2  b gibt an, um wieviele LE der Graph in y-Richtung verschoben ist. Am Scheitelpunkt S(0/b) kann man die Verschiebungskonstante erkennen.  in y-Richtung   verschobene  Normalparabel  y = x2 +  b   gestreckte / gestauchte  Parabel ohne Verschiebung  y =  a  • x2  gestreckte / gestauchte  Parabel mit y-Verschiebung  y =  a •x2 +  b
Den Faktor  a  nennt man  Streckungsfaktor. Er gibt an, um wieviel der Graph, die Parabel in y-Richtung gestreckt oder gestaucht ist. Ist a negativ, so ist die Parabel gestürzt (unten offen).  Normalparabeln  werden mit Schablonen gezeichnet. Man erkennt Sie an folgendem Sachverhalt:  Für .. LE in x-Richtung vom Scheitelpunkt aus  1   2   3   ...   sind es .. LE in y-Richtung vom Scheitelpunkt aus   1   4   9   ...  Gestreckte / gestauchte Parabeln müssen punktweise konstruiert werden. Die Schnittpunkte des Graphen mit der x-Achse nennt man Nullstellen N(?/0) ihr y-Wert ist immer 0.

---

Gemischtquadratische Funktion:   Lösungsvariable (x) kommt in der 1. und 2. Potenz vor
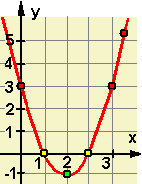	Der Graph einer gemischtquadratischen Funktion ist eine Parabel, die in der x-Richtung und in y-Richtung verschoben sein kann. Hier erfolgt die Einschränkung auf Normalarabeln, was es ermöglicht, aus der Scheitelform mit Hilfe der Normalparabel- Schablone den Graphen über den Scheitelpunkt zu zeichnen.  Normalform   Scheitelform  Scheitelpunkt    y = x2 +  ax + b   y = (x - d)2 +  c   S(d/c)   Es folgt ein konretes Beispiel wie abgebildet gelöst  von Scheitelpunkt über Scheitelform zur Normalform  (also hier schrittweise von rechts nach links).   y = x2 -  4x + 3    y = (x - 2)2  -1  S(2/-1)
Die Schnittpunkte des Graphen mit der x-Achse nennt man Nullstellen N(?/0). Ihr y-Wert ist immer 0. Die Lösung einer gemischtquadratischen Gleichung entspricht der Nullstellen-Berechnung. Die entsprechende Parabel hat je nach y-Verschiebung 2, eine oder keine Nullstelle(n). Die dazu passende quadratische Gleichung hat dementsprechend 2, eine oder keine Lösung(en).

Allgemeine Tipps: Mit der Tabulatortaste gelangt man jeweils ins jeweils nächste Eingabefeld der Übungsaufgaben. Leerzeichen werden als Fehler gewertet und 100% gibt es nur, wenn vor dem Prüfen alle Felder richtig ausgefüllt sind.

Diese Seite drucken

© 2006

Fenster schließen